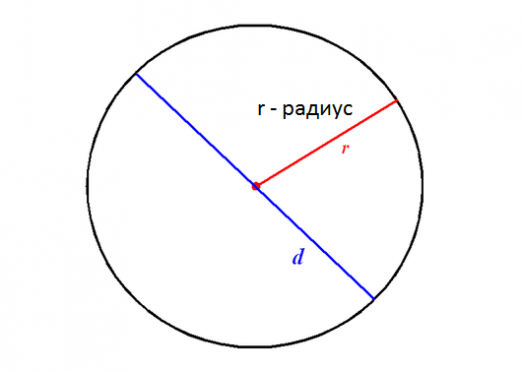
¿Cómo encontrar el radio del círculo inscrito?

El círculo está inscrito en los bordesun polígono regular, en caso de que se encuentre dentro de él, tocando líneas rectas que pasan por todos lados. Considera cómo encontrar el centro y el radio de un círculo. El centro del círculo será el punto en el que las bisectrices de los ángulos del polígono se cruzan. El radio se calcula: R = S / P; S es el área del polígono, P es el semiperímetro del círculo.

En el triángulo

En el triángulo rectángulo, ingrese solo un círculo, cuyo centro se llama centro; Se elimina de todos los lados por la misma distancia y es la intersección de las bisectrices.

R = (v3 / 6) a - el radio del círculo se puede calcular a partir de esta fórmula. En este caso, a es la longitud de su lado.

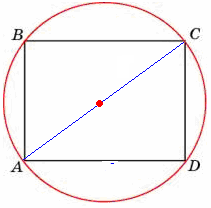
En un cuadrilátero

A menudo tenemos que decidir cómo encontrar el radiocírculo inscrito en esta figura geométrica. Debe ser convexo (si no hay auto intersección). Un círculo puede inscribirse en él solo si las sumas de lados opuestos son iguales: AB + CD = BC + AD.

El centro del círculo inscrito, el centrodiagonales, están ubicadas en una línea (según el teorema de Newton). El segmento, cuyos extremos se encuentran donde se cruzan los lados opuestos del cuadrilátero regular, se encuentran en la misma línea recta, llamada línea Gauss. El centro del círculo es el punto en el que las alturas del triángulo se cruzan con vértices, diagonales (según el teorema de Brokar).

En el rombo

Se consideran un paralelogramo con la misma longitud de lados. El radio del círculo inscrito en él se puede calcular de varias maneras.

1. Para hacer esto correctamente, encuentre el radiocírculo inscrito de un rombo, si se conoce el área del diamante, la longitud de su lado. Se usa la fórmula r = S / (2Xa). Por ejemplo, si el área del diamante es de 200 mm cuadrados, la longitud del lado es de 20 mm, luego R = 200 / (2X20), es decir, 5 mm.
2. El ángulo agudo de uno de los vértices es conocido. Entonces es necesario usar la fórmula r = v (S * sin (α) / 4). Por ejemplo, con un área de 150 mm y un ángulo conocido de 25 grados, R = v (150 * sen (25 °) / 4) ≈ v (150 * 0.423 / 4) ≈ v15.8625 ≈ 3.983 mm.
3. Todos los ángulos en el rombo son iguales. En esta situación, el radio del círculo inscrito en el rombo será igual a la mitad de la longitud de un lado de esta figura. Si discutimos sobre Euclides, quien dice que la suma de los ángulos de cualquier cuadrilátero es de 360 ​​grados, entonces un ángulo será de 90 grados; es decir. obtenemos un cuadrado

Ahora, después de que hemos revisado todofórmulas para calcular el radio de los círculos, puede calcular independientemente cualquier radio y compartir sus conocimientos con amigos y conocidos. Además, estas fórmulas te serán útiles en la escuela cuando resuelvas problemas geométricos complejos. En el instituto, estos znniya tampoco serán superfluos. Buena suerte con el cálculo de los radios!