Propiedades de un triángulo isósceles
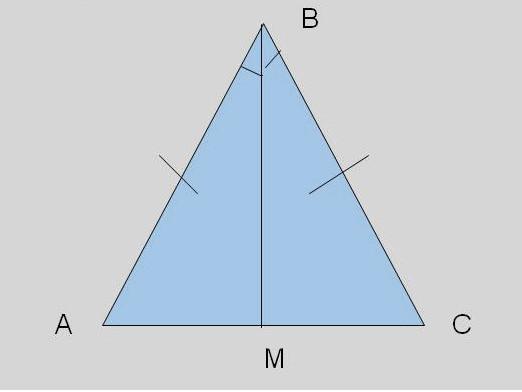
Un triángulo cuyos dos lados son iguales entrese llama isósceles. Estos lados se llaman laterales, y el tercer lado se llama base. En este artículo, le diremos sobre las propiedades de un triángulo isósceles.
Teorema 1
Los ángulos cerca de la base de un triángulo isósceles son iguales entre sí
Prueba del teorema
Supongamos que tenemos un triángulo isóscelesABC, cuya fundación es AB. Miremos el triángulo BAC. Estos triángulos, por el primer signo, son iguales entre sí. Lo es, porque BC = AC, AC = BC, ángulo ACB = ángulo de ACB. Por lo tanto, se deduce que el ángulo BAC = el ángulo ABC, porque estas son las esquinas de nuestros triángulos iguales. Aquí está la propiedad de los ángulos de un triángulo isósceles.
Teorema 2
La mediana en el triángulo isósceles, que se llevó a su base, también es la altura y bisectriz
Prueba del teorema
Supongamos que tenemos un triángulo isóscelesABC, cuya base AB y CD - es el medio que llevamos a cabo a la base. Los triángulos ACD BCD y CAD ángulo = ángulo CDB, ya que los ángulos correspondientes en la base de un triángulo isósceles (Teorema 1). Un lado de la AC = BC (por definición de un triángulo isósceles). Lateral AD = lado BD, después del punto D divide el segmento AB en partes iguales. Esto implica que el triángulo ACD = triángulo BCD.
De la igualdad de estos triángulos tenemosigualdad de las esquinas Es decir, el ángulo ACD = la esquina del BCD y el ángulo ADC = la esquina del BDC. De la igualdad 1 se deduce que el CD es una bisectriz. Y el ángulo ADC y el ángulo BDC son ángulos adyacentes, y se deduce de la igualdad 2 que ambos son rectos. Resulta que CD es la altura de un triángulo. Esta es la propiedad de la mediana de un triángulo isósceles.
Y ahora un poco sobre los signos de un triángulo isósceles.
Teorema 3
Si en un triángulo dos ángulos son iguales entre sí, entonces dicho triángulo es isósceles
Prueba del teorema
Supongamos que tenemos un triángulo ABC, en el cualángulo CAB = esquina de CBA. Triángulo ABC = triángulo BAC por el segundo signo de igualdad entre triángulos. Lo es, porque AB = BA; ángulo CBA = ángulo CAB, ángulo CAB = ángulo CBA. De esta igualdad de triángulos tenemos la igualdad de los lados correspondientes del triángulo - AC = BC. Entonces resulta que el triángulo ABC es isósceles.
Teorema 4
Si en cualquier triángulo su mediana es también su altura, entonces dicho triángulo es isósceles
Prueba del teorema
En el triángulo ABC, dibujamos la mediana del CD. También será la altura. Triángulo rectangular ACD = triángulo rectangular BCD, ya que el CD es común para ellos, y el cátodo AD = el BD. Se deduce que su hipotenusa es igual a la otra, como las partes correspondientes de triángulos iguales. Esto significa que AB = BC.
Teorema 5
Si los tres lados del triángulo son iguales a los tres lados del otro triángulo, entonces estos triángulos son iguales
Prueba del teorema
Supongamos que tenemos un triángulo ABC y un triángulo A1B1C1 tal que los lados AB = A1B1, AC = A1C1, BC = B1C1. Consideramos la demostración de este teorema por contradicción.
Supongamos que estos triángulos no son iguales entrepor ti mismo Por lo tanto tenemos que el ángulo BAC no es igual a la B1A1C1 ángulo, el ángulo ABC no es igual a la A1B1C1 ángulo, el ángulo ACB no es igual a la A1C1B1 ángulo simultáneamente. De lo contrario, estos triángulos son iguales sobre la base de considerado anteriormente.
Supongamos que el triángulo A1B1C2 = triánguloABC. En el triángulo, el vértice C2 se encuentra con el vértice C1 relativo a la línea A1B1 en un medio plano. Supusimos que los vértices C2 y C1 no coinciden. Supongamos que el punto D es el punto medio de C1C2. Así que tenemos triángulos isósceles B1C1C2 y A1C1C2, que tienen una base común C1C2. Resulta que sus medianas B1D y A1D también son sus alturas. Esto significa que la línea recta B1D y la línea recta A1D son perpendiculares a la línea recta C1C2.
B1D y A1D tienen diferentes puntos B1 y A1, y, en consecuencia, no pueden coincidir. Pero, de hecho, a través del punto D de C1C2, podemos dibujar una sola línea recta perpendicular a él. Tenemos una contradicción
¡Ahora sabes cuáles son las propiedades de un triángulo isósceles!