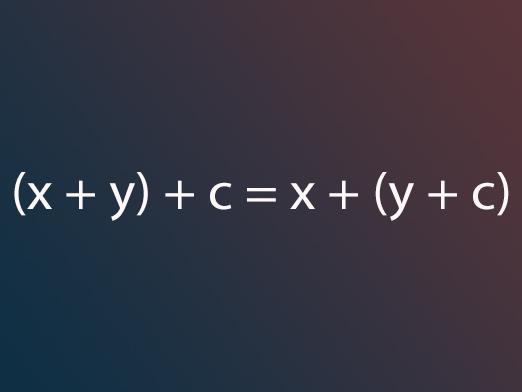Reglas para agregar vectores

Para realizar la operación de adiciónvectores, hay varias formas, que, dependiendo de la situación y el tipo de vectores considerados, pueden ser más cómodos de usar. Veamos las reglas para agregar vectores:

Regla del triángulo

La regla del triángulo es la siguiente: para agregar dos vectores x, y es necesario construir un vector x de modo que su origen coincida con el final del vector y. Entonces su suma será el valor del vector z, y el origen del vector z coincidirá con el comienzo del vector x, y el final con el final del vector y.

La regla del triángulo ayuda, si el número de vectores que deben sumarse no es más que dos.

Regla de un polígono

La regla del polígono es la más simple y más convenientepara agregar cualquier número de vectores en un avión o en el espacio. La esencia de la regla es la siguiente: al agregar vectores, debe alinearlos uno por uno secuencialmente para que el comienzo del vector posterior coincida con el final del anterior, y el vector que cierra la curva formada sea la suma de los términos de los vectores. Esto se ilustra gráficamente mediante la ecuación w = x + y + z, donde el vector w es la suma de estos vectores. Además, debe notarse que la suma no cambia del cambio en los lugares de los términos de los vectores, es decir (x + y) + z = x + (y + z).

La regla del paralelogramo

La regla del paralelogramo se usa para agregarvectores que se originan desde un solo punto. En esta regla, se dice que la suma de los vectores xey, que tiene un comienzo en un punto, será el tercer vector z originario también de este punto, y los vectores xey son los lados del paralelogramo, y el vector z es su diagonal. En este caso, tampoco importa en qué orden se agregarán los vectores.

Por lo tanto, la regla de polígono, la regla de triángulo y la regla de paralelogramo ayudan a resolver el problema de agregar vectores de absolutamente cualquier complejidad, tanto en el plano como en el espacio.