¿Cómo encontrar los ángulos de un triángulo?

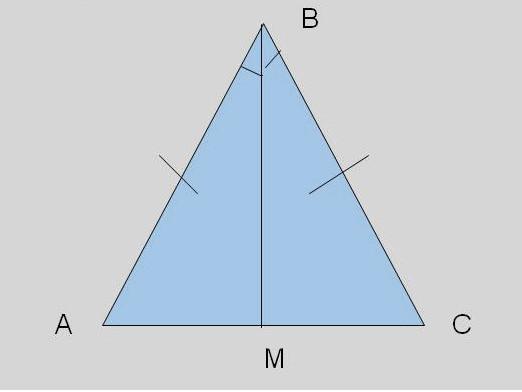
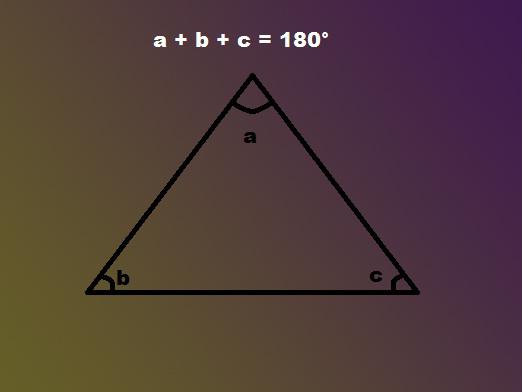
Probablemente todos conozcan una figura tan simple,que consiste en tres líneas interconectadas, como un triángulo. Desde el programa de la escuela todavía se conoce a todos cómo encontrar los lados del triángulo, pero hoy en día pocas personas recuerdan esas reglas y fórmulas verdaderas. Y actualizarlo en la memoria, no dolería en absoluto, porque a veces solo es necesario conocer las reglas de cómo encontrar ángulos en un triángulo para determinar una cierta distancia en la vida cotidiana.

Tratemos de recordar el Teorema de Pitágoras,que indica que el cuadrado de la hipotenusa es igual a la suma de los cuadrados de las dos patas. Nos referimos a los lados de un triángulo como travesaños que se cruzan en un ángulo de 90 grados. Hipotenusa es el lado entre ellos. Sabiendo la longitud de los dos lados, puede calcular el tercero de la fórmula.

Hay varias reglas más, cómo encontrar la terceraángulo de un triángulo, pero estos teoremas son un poco más complicados. Partiendo del teorema del seno, los lados del triángulo son proporcionales a los senos de los ángulos opuestos. Es decir, hay una fórmula según la cual el radio de un círculo circunscrito a un triángulo, multiplicado por dos, es igual a la relación entre cada lado del triángulo y el seno del ángulo opuesto. Conociendo los datos, puede calcular los lados faltantes. También se puede recurrir al teorema del coseno, que generaliza el mismo teorema de Pitágoras. El cuadrado de un lado es igual a la suma de los cuadrados de los otros dos menos el producto doblado de estos lados por el coseno del ángulo entre ellos.

La más importante de todas estas fórmulas es poder sustituir correctamente los datos y encontrar lo desconocido, ya que la derivación incorrecta de lo desconocido no dará el resultado correcto.