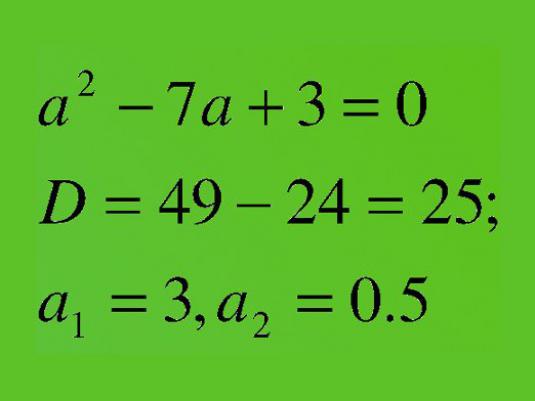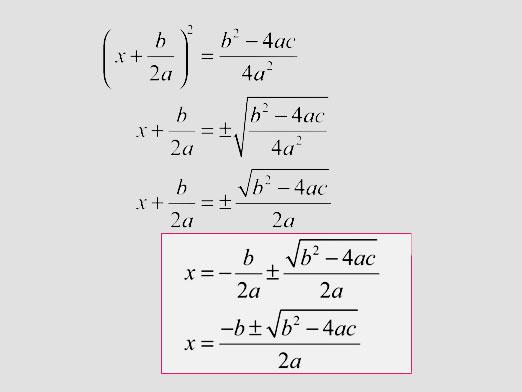Cómo resolver la ecuación cuadrática

La ecuación cuadrática completa se resuelve al encontrar su discriminante.
Recuerde que una ecuación cuadrática completa es una ecuación de la forma rx2+ wx + h = 0, donde r, w, h son los coeficientes de la ecuación cuadrática: algunos números no son iguales a cero, yx es una variable (desconocida).
Cómo resolver la ecuación cuadrática a través del discriminante
Calcula el discriminante (D) de la ecuación cuadrática. Para calcular el discriminante, reste el producto de los coeficientes r y h por 4 del segundo coeficiente w, elevado a la segunda potencia.
D = w2- 4rh
Si el discriminante resultante de la ecuación cuadrática es menor que cero (D <0), entonces esta ecuación no tiene raíces, y por lo tanto no tiene solución.
Si el discriminante resultante de un cuadradola ecuación es cero (D = 0), entonces la ecuación tiene solo una raíz. Para calcular esta raíz, es necesario dividir el coeficiente de la ecuación cuadrática w con el signo menos por el doble del coeficiente r.
Esta es la fórmula para encontrar una sola raíz:
x = -w / 2r
Si el discriminante resultante de la ecuación cuadrática es mayor que cero (D> 0), entonces dos raíces se aproximan a la ecuación.
Para encontrar la primera raíz de la ecuación cuadrática x1, es necesario agregar la raíz cuadrada del discriminante al coeficiente w con un signo menos, y dividir el resultado por el doble del coeficiente r.
Para encontrar la segunda raíz de la ecuación x2Se debe restar de la raíz cuadrada del coeficiente discriminante w con el signo menos, y el resultado se divide por el coeficiente r duplicado.
Si la ecuación cuadrática completa de la forma rx2+ wx + h = 0 se reduce, es decir, el coeficiente junto a lo desconocido en la segunda potencia es igual a la unidad (r = 1), luego es posible resolverlo mediante la fórmula del teorema de Viet.
Cómo resolver la ecuación cuadrática reducida usando la fórmula del teorema de Vieta
Vieta teorema es como sigue: la suma de las raíces de una ecuación cuadrática Esta engañosa igual al segundo factor, pero con el signo opuesto, y el producto de las raíces es igual al término constante.
Es decir, si una ecuación de la forma rx2+ wx + h = 0 tiene raíces reales, luego
- x1 + x2 = -w
- x1 * x2 = h
A partir de estas fórmulas uno puede tratar de adivinar las raíces de la ecuación. Para este fin, necesitamos expandir el término libre h en dos factores, la suma de los cuales sería igual al coeficiente w con el signo opuesto.
Por ejemplo
Tomamos la ecuación reducida x2- 8x + 12 = 0
Sabemos que:
- x1 + x2 = 8
- x1 * x2 = 12
Necesitamos descomponer 12 en dos de esos factores, que juntos dan 8. Es obvio que 6 y 2 son tales factores.
De hecho:
- 6 * 2 = 12
- 6 + 2 = 8
Por lo tanto, se deduce que los números 6 y 2 son verdaderosraíces para la ecuación cuadrática reducida. Tales soluciones obvias vienen rápidamente a la mente cuando se trabaja con coeficientes enteros simples de la ecuación cuadrática. por lo tanto, el teorema de Vieta se usa a menudo para seleccionar las raíces de las ecuaciones cuadráticas, lo que ahorra un tiempo considerable al resolverlas.