¿Cómo encontrar el área de una figura?

Saber y ser capaz de calcular las áreas de diferentelas figuras son necesarias no solo para resolver problemas geométricos simples. No prescinda de este conocimiento y cuando elabore o verifique las estimaciones para la reparación de las instalaciones, calcule la cantidad de suministros necesarios. Así que descubramos cómo encontrar las áreas de diferentes figuras.

Area

La parte del plano dentro de un contorno cerrado se denomina área de este plano. El área se expresa por la cantidad de unidades cuadradas encerradas en ella.

Para calcular el área de las formas geométricas básicas, debe usar la fórmula correcta.

El área del triángulo

Notación:

• S es el área requerida,
• a, b, c son las longitudes de los lados del triángulo,
• h es la altura del triángulo deseado,
• γ es el ángulo entre el lado ay el lado b,
• r es el radio del círculo (inscrito en un triángulo),
• R es el radio del círculo (descrito alrededor del triángulo),
• p es la mitad del perímetro del triángulo.

1. Si se conocen h, a, entonces el área del triángulo deseado se define como el producto de la longitud del lado y la altura del triángulo caído a este lado, dividido por la mitad: S = (a · h) / 2
2. Si a, b, c se conocen, entonces el área requeridacalculado por la fórmula de Heron: la raíz cuadrada tomada de los productos de la mitad del perímetro del triángulo y las tres diferencias medias y el perímetro de cada lado del triángulo: S = √ (p · (p - a) · (p - b) · (p - c)).
3. Si a, b, γ se conocen, entonces el área del triángulo se define como la mitad del producto de 2 lados multiplicado por el valor del ángulo sinusal entre estos lados: S = (a · b · sin γ) / 2
4. Si se conocen a, b, c, R, el área deseada se define como el producto de las longitudes de todos los lados del triángulo por los cuatro radios del círculo circunscrito: S = (a · b · c) / 4R
5. Si se conocen p, r, entonces el área requerida del triángulo se determina multiplicando la mitad del perímetro por el radio del círculo inscrito en él: S = p · r

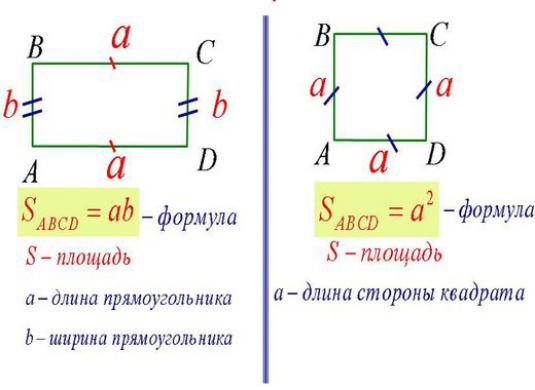
Cuadrado de un cuadrado

Notación:

• S es el área requerida,
• a es la longitud del lado,
• d es la longitud de la diagonal.

1. Si se conoce el lado, entonces el área de esta figura se define como el cuadrado de su longitud lateral: S = a²
2. Si se conoce d, entonces el cuadrado del cuadrado se define como la mitad del cuadrado de la longitud de su diagonal: S = d²/ 2

Área del rectángulo

Notación:

• S es el área a determinar,
• a, b son las longitudes de los lados del rectángulo.

1. Si se conocen a, b, entonces el área de este rectángulo está determinada por el producto de las longitudes de sus dos lados: S = a · b
2. Si las longitudes de los lados son desconocidas, entonces el área del rectángulo debe dividirse en triángulos. En este caso, el área del rectángulo se define como la suma de las áreas de sus triángulos constituyentes.

El área del paralelogramo

Notación:

• S es el área requerida,
• a, b son las longitudes de los lados,
• h es la longitud de la altura de este paralelogramo,
• d1, d2 son las longitudes de dos diagonales,
• α es el ángulo entre los lados,
• γ es el ángulo entre las diagonales.

1. Si a, h se conocen, entonces el área deseada se determina multiplicando las longitudes de los lados y la altura caída en este lado: S = a · h
2. Si se conocen a, b, α, entonces el área del paralelogramo se determina multiplicando las longitudes de los lados del paralelogramo y el valor sinusoidal del ángulo entre estos lados: S = a · b · sin α
3. Si sabemos d₁, d₂, γ, entonces el área del paralelogramo se define como la mitad del producto de las longitudes diagonales y el valor del seno del ángulo entre estas diagonales: S = (d₁· D₂· Sinγ) / 2

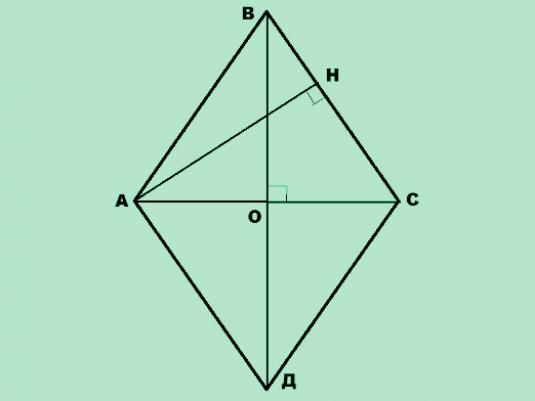
Diamond Square

Notación:

• S es el área requerida,
• a es la longitud del lado,
• h es la longitud de la altura,
• α es el ángulo más pequeño entre los dos lados,
• d1, d2 son las longitudes de dos diagonales.

1. Si se conocen a, h, entonces el área del rombo se determina multiplicando la longitud del lado por la longitud de la altura que se baja a este lado: S = a · h
2. Si a, α se conocen, entonces el área rómbica se determina multiplicando el cuadrado de la longitud del lado por el seno del ángulo entre los lados: S = a²· Sin α
3. Si sabemos d₁ yd₂, entonces el área requerida se define como la mitad del producto de las longitudes de los diamantes del rombo: S = (d₁· D₂) / 2

Área del trapecio

Notación:

• S es el área requerida,
• a, b - longitudes de 2 bases del trapecio,
• c, d son las longitudes de los lados izquierdo y derecho del trapecio,
• h es la altura del trapecio,

1. Si se conocen a, b, c, d, el área requerida se determina mediante la fórmula: S = (a + b) / 2 * √ [c²- (((b-a)²+ c²-d²) / (2 (b-a))²]
2. Para saber a, b, h, el área requerida se define como el producto de la mitad de la suma de las bases y la altura del trapecio: S = (a + b) / 2 · h

Área de un cuadrilátero convexo

Notación:

• S es el área requerida,
• d₁, d₂ - las longitudes de las diagonales de un cuadrilátero dado,
• α es el ángulo entre las diagonales,
• p = (a + b + c + d) / 2 es la mitad del perímetro del cuadrilátero convexo,
• ayb, cyd son las longitudes de cada lado del cuadrilátero convexo,
• θ = (α + β) / 2 es la mitad de la suma de dos ángulos opuestos de un cuadrángulo convexo,
• r es el radio del círculo inscrito en un cuadrilátero convexo.

1. Si sabemos d₁, d₂, α, entonces el área del cuadrilátero convexo se define como la mitad del producto de las diagonales del cuadrilátero multiplicado por el ángulo sinusal entre estas diagonales: S = (d₁· D ₂· Sin α) / 2
2. Para p, r conocido, el área del cuadrilátero convexo se define como el producto del semiperímetro del cuadrilátero por el radio del círculo inscrito en este cuadrilátero: S = p · r
3. Si a, b, c, d, θ se conocen, entonces el área de la convexidadcuadrilátero se define como la raíz cuadrada de los productos de la diferencia en el medioperímetro y la longitud de cada lado menos el producto de las longitudes de todos los lados y el cuadrado del coseno de la mitad de la suma de dos ángulos opuestos: S² = (p - a) (p - b) (p - c) (p - d) - abcd · cos²((α + β) / 2)

Área del círculo

Notación:

• S es el área requerida,
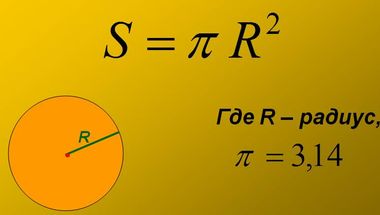
• r es la longitud del radio,
• d es la longitud del diámetro.

Si se conoce r, entonces el área deseada se define como el producto del número π por el radio en el cuadrado: S = π r²

Si se conoce d, entonces el área del círculo se define como el producto del número π por el cuadrado del diámetro, dividido por cuatro: S = (π · d²) / 4

El área de una figura compleja

Un complejo se puede dividir en figuras geométricas simples. El área de una figura compleja se define como la suma o diferencia de las áreas constituyentes. Considera, por ejemplo, un anillo.

Designación:

• S es el área del anillo,
• R, r son los radios de la circunferencia externa e interna, respectivamente,
• D, d son los diámetros del círculo exterior y la circunferencia interior, respectivamente.

Para encontrar el área del anillo, es necesario tomar el área

círculo más pequeño S = S1-S2 = πR²-rr² = π (R²-r²)

Por lo tanto, si se conocen R y r, entonces el área del anillo se define como la diferencia de los cuadrados de los radios de los círculos exterior e interior multiplicados por el número pi: S = π (R²-r²)

Si se conocen D y d, entonces el área del anillo se define como un cuarto de la diferencia en los cuadrados de los diámetros de los círculos externo e interno multiplicado por el número pi: S = (1/4) (D²-d²) π.

El área de la figura sombreada

Supongamos que hay otro (B) (más pequeño) dentro del mismo cuadrado (A), y tenemos que encontrar la cavidad sombreada entre las figuras "A" y "B". Digamos el "marco" de un cuadrado pequeño. Para hacer esto:

1. Encontramos el área de la figura "A" (calculada por la fórmula para encontrar el cuadrado del cuadrado).
2. Del mismo modo, encontramos el área de la figura "B".
3. Restamos el área "B" del área "A". Y así obtenemos el área de la figura sombreada.

Ahora sabes cómo encontrar áreas de diferentes formas.