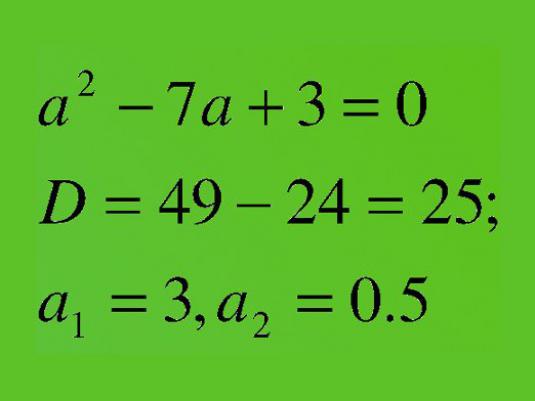¿Qué es una ecuación?

Aquellos que dan los primeros pasos en álgebra, por supuesto,la entrega ordenada del material es obligatoria. Por lo tanto, en nuestro artículo que tal ecuación, no solo damos una definición, sino que también damos varias clasificaciones de ecuaciones con ejemplos.

¿Qué es una ecuación? Conceptos generales

Entonces, la ecuación es una especie de igualdad condesconocido, denotado por una letra latina. En este caso, el valor numérico de esta letra, que permite obtener la igualdad correcta, se denomina raíz de la ecuación. Puedes leer más sobre esto en nuestro artículo. Cuál es la raíz de la ecuación, continuaremos la conversación sobre las ecuaciones mismas. Los argumentos de la ecuación (o variables) se llaman incógnitas, y la solución de la ecuación es el hallazgo de todas sus raíces o la ausencia de raíces.

Tipos de ecuaciones

Las ecuaciones se dividen en dos grandes grupos: algebraico y trascendental.

• Algebraico es tal ecuación, enque se utiliza para encontrar la raíz de la ecuación solo acciones algebraicas - 4 aritmética, así como aumentar la potencia y extraer la raíz natural.
• Una ecuación se llama trascendental, en la que las funciones no algebraicas se utilizan para encontrar la raíz: por ejemplo, funciones trigonométricas, funciones logarítmicas y otras.

Entre las ecuaciones algebraicas, también distinguimos:

• todo - con ambas partes, que consiste en expresiones algebraicas enteras en relación con lo desconocido;
• fraccional que contiene expresiones algebraicas enteras en el numerador y el denominador;
• Irracional: las expresiones algebraicas se encuentran bajo el signo de la raíz.

También observamos que las ecuaciones fraccionarias e irracionales pueden reducirse a resolver ecuaciones completas.

Las ecuaciones trascendentales se dividen en:

• Indicativo: estas son las ecuaciones quecontener una variable en el exponente. Se resuelven moviéndose a una única base o exponente, poniendo un multiplicador común por paréntesis, factorización y algunas otras formas;
• Ecuaciones logarítmicas con logaritmos, luegohay ecuaciones donde las incógnitas están dentro de los logaritmos mismos. Es muy difícil resolver tales ecuaciones (a diferencia de, digamos, la mayoría de las algebraicas), ya que esto requiere una preparación matemática sólida. Lo más importante aquí es pasar de la ecuación con los logaritmos a la ecuación sin ellos, es decir, simplificar la ecuación (esta forma de eliminar los logaritmos se llama potenciación). Por supuesto, es posible potenciar la ecuación logarítmica solo si tienen bases numéricas idénticas y no tienen coeficientes;
• Trigonométricas son ecuaciones con variables bajo los signos de funciones trigonométricas. Su solución requiere el dominio inicial de las funciones trigonométricas;
• mixto - estas son ecuaciones diferenciadas con partes que pertenecen a diferentes tipos (por ejemplo, con partes parabólicas y elípticas o elípticas e hiperbólicas, etc.).

En cuanto a la clasificación por el número de incógnitas,entonces todo es simple: distingue ecuaciones con uno, dos, tres, etc. desconocido. También hay otra clasificación, que se basa en el grado que existe en el lado izquierdo del polinomio. A partir de esto, se distinguen las ecuaciones lineales, cuadradas y cúbicas. Las ecuaciones lineales también se pueden llamar ecuaciones del 1 ° grado, cuadrado - 2 ° y cúbico, respectivamente, 3 °. Bien, ahora damos ejemplos de las ecuaciones de un grupo en particular.

Ejemplos de diferentes tipos de ecuaciones

Ejemplos de ecuaciones algebraicas:

• ax + b = 0
• hacha³+ bx²+ cx + d = 0
• hacha⁴+ bx³+ cx²+ bx + a = 0
  (a no es 0)

Ejemplos de ecuaciones trascendentales:

• cos x = x lg x = x-5 2^x= lgx + x⁵+40

Ejemplos de ecuaciones enteras:

• (2 + x) 2 = (2 + x) (55x-4) (x2-12x + 10) 4 = (3x + 10) 4 (4x2 + 3x-10) 2 = 9x4

Ejemplo de ecuaciones fraccionales:

• 15 x + - = 5x - 17 x

Un ejemplo de ecuaciones irracionales:

• √2kf (x) = g (x)

Ejemplos de ecuaciones lineales:

• 2x + 7 = 0 x - 3 = 2 - 4x 2x + 3 = 5x + 5 - 3x - 2

Ejemplos de ecuaciones cuadráticas:

• x²+ 5x-7 = 0 3x²+ 5x-7 = 0 11x²-7x + 3 = 0

Ejemplos de ecuaciones cúbicas:

• x³-9x²-46x + 120 = 0 x³- 4x²+ x + 6 = 0

Ejemplos de ecuaciones exponenciales:

• 5^{x + 2}= 125 3^x· 2^x= 8^{x + 3} 3^2x+ 4 · 3^x-5 = 0

Ejemplos de ecuaciones logarítmicas:

• registro₂x = 3 log₃x = -1

Ejemplos de ecuaciones trigonométricas:

• 3sin²x + 4sin x cosx + cos²x = 2 sin (5x + π / 4) = ctg (2x-π / 3) sinx + cos²x + tg³x = ctg⁴x

Ejemplos de ecuaciones mixtas:

• registro_x(log₉(4⋅3^x-3)) = 1 | 5x-8 | + | 2⋅5x + 3 | = 13

Queda por agregar que para resolver ecuacionesdiferentes tipos aplican una variedad de métodos. Bueno, para resolver casi cualquier ecuación, se requerirá conocimiento no solo de álgebra sino también de trigonometría, y el conocimiento a menudo es muy profundo.